Formula Quick Look

The following page is a list of formulas and very brief explanations.

Density is the ratio of a substance's mass to its volume and can be expressed mathematically as

D=M/V

where D is density, M is mass, and V is volume.

Example:

What is the density of an object having a mass of 8 kg and a volume of 2 cubic meters?
D = M/V
D = 8/2
D = 4 kg/m³

Temperature:
In science, we will use Celsius or Kelvin temperature scales to describe temperature.

To convert between Celsius and Kelvin:

Kelvin = Celsius + 273.15
Celsius = Kelvin - 273.15

To convert between Celsius and Fahrenheit:

Fahrenheit = Celsius * (9/5) + 32
Celsius = (Fahrenheit - 32) * 5/9

Gas Laws:

Charles's Law
The volume of a gas is directly proportional to its temperature in kelvins if the pressure and number of molecules are constant.

V1T1=V2T2  

Boyle's Law
The volume of a gas is inversely proportional to its pressure if the temperature and the number of molecules are constant.

P1V1=P2T2

Combined Gas Law
Pressure is inversely proportional to volume, or higher volume equals lower pressure. Pressure is directly proportional to temperature, or higher temperature equals higher pressure.

(P1V1)/T1=(P2V2)/T2 

Example:

If a sample of gas initially has a pressure of 2 atm, a volume of 3 liters, and a temperature of 300 K, what would its final volume be if the pressure changed to 1.5 atm and the temperature changed to 290 K? 

(P1V1)/T1=(P2V2)/T2 (2 • 3)/300 = (1.5 • V)/290
6/300 = 1.5 V/290
290 • (6/300) = 1.5 V
5.8 = 1.5 V
5.8/1.5 = V
3.87 l = V

Ideal Gas Law

When the number of molecules are included in calculations, the following formula can be used:

PV = nRT

This law can be converted into the following form which will allow memorization of only 1 formula for gas law problems:

P1V1     P2V2
_____ = _____
n1T1       n2T2 

Motion:

Finding final velocity:

vf = vi + at

where vf is final velocity, vi is initial velocity, a is acceleration, and t is elapsed time.

Example:

An object is moving at a rate of 3 m/s and accelerates at a rate of 2 (m/s)/s for 5 seconds. What is its final velocity? 

vf = vi + at
vf = 3 + 2 • 5
vf = 3 + 10
vf = 13 m/s

Finding average velocity:

v(ave) = (vf+vi)/2

where v(ave) is average velocity, vf is final velocity, and vi is initial velocity. Also:

v(ave) = ((vi + at) + vi)/2

Finding final position (final distance from a reference point):

df = di + vit + 1/2at²         

where df is the final, total displacement… 

di is the initial displacement. (How far from whatever point of reference is the object when the thing starts accelerating?)…

 vi is the initial velocity of the object at the beginning of the acceleration.

t is the elapsed time from the beginning of the acceleration until the end of the period being observed. 

(vit accounts for the motion of the object based on its starting velocity. It keeps covering distance at the initial rate, and additionally, it accelerates and covers more distance.) 

a is the acceleration and t is elapsed time.

Example:

An object begins 10 meters from a mark on a track with an initial velocity of 3 m/s. If it accelerates at a rate of 5 (m/s)/s for 4 seconds, how far from the mark does it end up? 

df = di + vit + 1/2at² 

df = 10 + 3(4) + 1/2(5)(4)^2
df = 10 + 12 + 1/2 (5) (16)
df = 10 + 12 + 40
df = 62 m

Force:

Where F is force, a is acceleration, and m is mass, then:

F = ma

Force of Friction—friction always opposes forces that are moving (or trying to move) an object.

Ff = Fnμ

where  Ff  is the force of friction,  Fn  is the normal force, and  μ is the coefficient of friction (a number that is looked up).

The normal force is the portion of weight that is perpendicular to the surface. For a flat surface (the angle between the surface and the horizon is zero, θ = 0):

Fn = mg

where m is mass and g is acceleration due to gravity (9.8 (m/s/)s on earth) 

Work and Energy:

Work is found by

W = Fd

where W is work, F is force applied (not net force!), and d is displacement/distance.

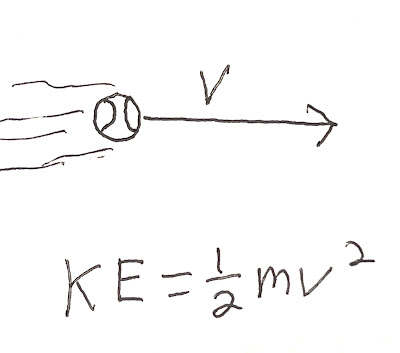
Kinetic energy (KE) is found with this equation:

KE = 1/2 mv²

where KE is kinetic energy, m is mass and v is velocity.


The potential gravitational energy can be found with this equation:

PE = mgh

where PE is potential gravitational energy, m is mass, g is acceleration due to gravity, and h is height.

On earth, acceleration due to gravity is 9.8 (m/s)/s


The amount of elastic potential energy is determined by how hard it is to compress or stretch something and how far it is stretched or compressed.

The equation to find this is:

PE = 1/2kd²

where PE is potential elastic energy, k is a constant specific to a particular stretchy thing (spring, rubber band, etc.) and d is the distance that it is stretched or compressed (sometimes x is used instead of d, as in the illustration)



Heat/Energy Transfer

Now to find heat, we can use the formula:

Q = mcΔT

Where Q is heat or thermal energy, m is mass, c is a number called specific heat that you either look up or calculate, and ΔT is the change in temperature.

EXAMPLES:

How much heat is absorbed by 200 grams of water that starts at 25C and ends up at 30C, given that the specific heat of water is 4.2 J/g°C?

Q = mcΔT

Q = 200•4.2•(30-25)

Q = 200•4.2•5

Q = 4200 J

What is the specific heat of a metal that has a mass of 50 grams and changes temperature from 100C to 30C and gives off 4200 J of thermal energy?

Q = mcΔT

4200 = 50•c•(100-30)

4200 = 50•70•c

4200 = 3500c

4200/3500 = c

1.2 = c

---

VARIOUS EXAMPLES

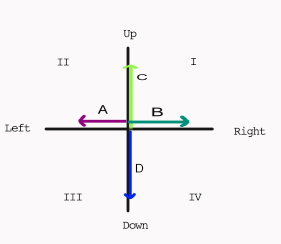
Given the following information, find the work done on a 6.5 kg object after 4 seconds:

A = 16 N
B = 4 N
C = 14 N
D = 9 N

 STEP 1: Find Net Force by resolving the UpDown forces, resolving the LeftRight forces, and then using the Pythagorean Theorem:


F(net)² = UpDown² + LeftRight²

F(net)² = (16 - 4)² +(14 - 9)²
F(net)² = (12)² + (5)²
F(net)² = 144 + 25
F(net)² = 169
F(net) = 13 N

STEP 2: Find Acceleration where the force is the net force on the object:

F = ma
13 = 6.5a
13/6.5 = a
2 (m/s)/s  =  a

STEP 3: Find the distance through which the force acted due to the net force.

df = 1/2at²
df = 1/2 • 2 • 4²
df = 16 m

STEP 4: Find the work done by the net force through the calculated distance.

W = Fd
W = 13 • 16
W = 208 J




To find the final velocity in the above:

Do Step 1 above.
Do Step 2 above.

STEP 3:

Vf = at
Vf = 2 • 4
Vf = 8 m/s


To find final kinetic energy, first find the final velocity (above), and then:

KE = 1/2mv²
KE = 1/2•6.5•8²
KE = 1/2 • 6.5 • 64
KE = 208 J

The Transfer of Thermal Energy

Thermal energy is a relatively easy concept to grasp. Objects in nature have a temperature, and that is (by definition) the average kinetic energy of the molecules of the object. The higher the temperature, the higher the average kinetic energy. Naturally, the larger the object, the more molecules, which means more kinetic energy.

So, thermal energy is a function of how many molecules are present as well as what the temperature of those molecules are. For any given substance, the total thermal energy can be easily found. 

The total thermal energy would be how much energy could be given off if the object's temperature dropped to absolute zero. This theoretical idea is not practical. 

Instead, thermal energy is generally defined as the amount of energy given off or taken in as a result of some change in temperature. 

The formula for finding thermal energy given a temperature change is actually very easy, EXCEPT it relies on the idea of change in temperature. It is common to use T for temperature and likewise common (though it is possibly something new to many introductory students) to use the Δ as a symbol for "change."

Thus, ΔT is the symbol for change in temperature.

So, if something starts off at 100 C and ends up at 80 C, what is ΔT?

ΔT = Ti - Tf

ΔT = 100 - 80

ΔT=20

Finding ΔT is more about getting used to the symbol than anything else; it is the difference between starting and ending (initial and final) temperatures.

Now to find heat, we can use the formula:

Q = mcΔT

Where Q is heat or thermal energy, m is mass, c is a number called specific heat that you either look up or calculate, and ΔT is the change in temperature.

So, what is specific heat? Different materials require different amounts of energy to change temperature. Specific heat is a measure of that difference. Specific heat is the amount of energy needed to raise one unit of mass (grams, for instance) one degree (usually Celsius). The energy is usually measured in Joules or Calories. 

EXAMPLES:

How much heat is absorbed by 200 grams of water that starts at 25C and ends up at 30C, given that the specific heat of water is 4.2 J/g°C?

Q = mcΔT

Q = 200•4.2•(30-25)

Q = 200•4.2•5

Q = 4200 J

What is the specific heat of a metal that has a mass of 50 grams and changes temperature from 100C to 30C and gives off 4200 J of thermal energy?

Q = mcΔT

4200 = 50•c•(100-30)

4200 = 50•70•c

4200 = 3500c

4200/3500 = c

1.2 = c

TRANSFER OF ENERGY

Thermal energy transfer is a fairly simple concept. When (two or more) things are in the same environment (which we will call being in the same system) the molecules of the things will bump into each other until all of them have the same kinetic energy.

What does that mean? Those things with higher energy will give off their energy to the things with lower energy. After a period of equalization, everything in the system will have the same average kinetic energy.

So, suppose a hot piece of metal is put into a cup of cool water… The energy from the metal will be transferred into the water. The metal will cool off. The water will warm up.

The amount of energy given off will be equal to the amount of energy absorbed. This is a major law of physics! Energy cannot be destroyed. It can change forms, or be transferred from one thing to another, but it cannot just go away.

Therefore, if hot metal is put into cool water, the quantity of the energy lost is equal to the quantity of the energy gained. Thus, Qlost = Qgained.

SO… if you know how much energy was gained, then you know how much energy was lost. 

And?

Suppose you put a sample of hot metal (for which you know the starting temperature) into water. If you know the mass of the water and you know the temperature change of the water, using the known quantity for water's specific heat (4.2), you can calculate how much energy was gained. Then, if you know the energy gained by the metal, the mass of the metal, and the change of temperature of the metal, you can then calculate the specific heat.

SUMMARY THOUGHTS

• Q = mcΔT
• In a system, once equilibrium is reached everything in the system will have the same kinetic energy (temperature).
• Energy lost from objects in a system will equal energy gained by other objects in the system until all of the objects have equal temperature.

VIRTUAL LAB

The following video presents a lab exercise in which the process of heat exchange is discussed and used.

Here is a link to the companion lab sheet: CLICK HERE 

https://www.youtube.com/watch?v=xhmeIMPeL04

Concepts of Force, Work, and Energy

The concepts of force, work, and energy are closely related, and they are often tied to motion. To begin understanding of how they interact, it is important to start with a firm grasp of the basic concepts.

FORCE

The starting place for understanding how force, work, and energy interact is to quickly review concepts related to force.

Force is a push or a pull that acts on something in creation.

Forces are the result of four fundamental forces found in creation: gravitational force, electromagnetic force, and the strong and weak forces associated at the atomic level.

At any given time, an object in the universe is subjected to many forces. Forces on an object add up as vectors (direction and magnitude), and if the net force is NOT zero, then the object will be accelerated at a rate given by Newton's second law:

F = ma

where F is the net force on an object, m is the mass of the object, and a is the resulting acceleration.

Force is measured in Newtons (the symbol is N), which is the potential to accelerate a 1 kg object at a rate of 1 meter per second per second. that is:

1 N = 1 (kg • m/s)/s = 1 kg • m/s²

It is important to remember that an object can be moving, but that the net force on it is zero. This does not mean there are no forces at work. It just means that it is moving at a steady rate (constant velocity) because all of the forces are balanced out. For example:

Pedaling a bicycle at a steady rate requires that the force of the tires pushing against the ground is equal to the wind resistance opposing the motion of the bike. 

When a box is pushed across the floor at a steady rate, the force pushing against the box is equal to the oppositional force of friction.

Consider the box example further. The force of gravity pulls the box toward the center of the earth, causing it to press against the floor. The solid nature of the floor opposes the force of gravity, keeping the box from moving downward. The "up and down" forces are in balance, and they create the resistance of friction that opposes the force exerted on the box to push it. If the pushing force is greater than the frictional force, then the box accelerates. If they pushing force is equal, the box moves at a steady rate. If the pushing force is less than the force of friction, the box slows down or does not start moving.

WORK

Extending the concept of force to motion, the idea of work emerges. 

In the context of physics, work is a very specific concept. Work is the quantity that represents the application of a force through a distance. This means that work is done when a force is exerted and when motion occurs. Pushing against a wall does no work, though it requires a lot of effort (which is a loosely used term related to work, force, and motion.

Work can be calculated as the product of force and distance/displacement:

W = Fd

where W is work, F is force applied (not net force!), and d is displacement/distance.

Work is measured in Newton-meters (the symbol is Nm or N-m) meaning that a Newton was applied through a distance of one meter.

So, back to the box example above, if the force to push the box causes it to move some distance, then work is done. If the force does not cause it to move, then effort was spent, but no work was done.

Assume the force needed to balance friction and move the box at a constant velocity is 5 N and that the box is pushed 10 m. In that case how much work was done?

W = Fd
W = 5N • 10 m
W = 50 Nm

It is vital to remember that work is done, not as a result of the net force, but rather as a result of the applied force through a distance. In the case of a box moving at a steady rate (constant velocity) the net force on the box is zero, but the applied force is used to find work done.

To make things slightly confusing, in many cases, (because of what is discussed below about energy), work will given the unit of joules (J). To extend the above example with this concept,

W = Fd

W = 5N • 10 m

W = 50 Nm

W = 50 J

ENERGY

Going to the next concept, energy, is not terribly difficult. Energy can be defined as the potential to do work.

There is, thus, a direct relationship between work and energy. However, where work is often described with the unit of Newton-meters, energy is generally described with the equivalent unit, joules (the symbol is J).

A joule is the energy needed to do 1 Newton-meter of work. So:

1 J = 1 Nm

An example will help clarify the relationship between work and energy. Think about this:

If "Cash" is the potential do "pay" and energy is the potential do work, then…

Q: If you paid $20.00 for something, how much cash did you spend?
A: You spent $20.00 

Q: If you did 20 Nm of work, how much energy did you spend?
A: You spent 20 Nm (or 20 J)

Thus, once you have calculated the amount of work done, you know how much energy was used to do it.


FORMS OF ENERGY

Up to this point, energy has been looked at in terms of motion and the potential to cause motion. However, energy exists on other forms. It is important to understand that energy can change forms.

Energy exists in different forms. Though it is still the potential to do work, as different forms of energy are examined, the idea of moving something through a distance can get lost. That should not be a distraction, though. Just cling to the idea that energy is the potential to do work.

Mechanical Energy—This is the form of energy that has been discussed up to this point.

Mechanical energy is the energy associated with the motion and position of everyday objects.

There are three TYPES of Mechanical Energy

In the sections that follow, three types of mechanical energy will be explored:

• Kinetic energy
• Gravitational potential energy
• Elastic potential energy

Kinetic Energy—the energy of motion is called kinetic energy.

The amount of energy a moving object has can be found based on the mass and velocity of the object that is moving. Kinetic energy (KE) is found with this equation:

KE = 1/2 mv²

where KE is kinetic energy, m is mass and v is velocity.

 

Potential Energy—energy that is stored as a result of position or shape.

Potential energy (PE) is a little more broad than kinetic energy. Potential energy can be thought of as how much motion could occur if the stored energy was released.

For instance, a hot wheel car at the top of the track is not moving, but if it is released, because of its position, gravity will cause it to start. The car will accelerate (overcoming friction of the track and in the bearings of the wheels) and move down the track.

Another type of potential energy relates to the shape of something. When you stretch a rubber band, because of its shape, it has stored, potential energy. Likewise a compressed or stretched spring, because of its shape, also has potential energy.

Two types of potential energy will  be examined more specifically.

Source: http://www.batesville.k12.in.us/

Gravitational Potential Energy—the potential to create motion based on position within gravity and on the mass of the object.

Imagine hanging a heavy weight over a pulley and attaching to a car. Letting the weight go would create tension in the rope and that tension would create a force on the car causing it to accelerate. The higher the weight, the more potential it would have. The heavier the weight, likewise, the more potential it would have.

The potential gravitational energy can be found with this equation:

PE = mgh

where PE is potential gravitational energy, m is mass, g is acceleration due to gravity, and h is height.

On earth, acceleration due to gravity is 9.81 (m/s)/s.

Source: http://hyperphysics.phy-astr.gsu.edu/hbase/pespr.html

Elastic Potential Energy—the potential energy of an object that is stretched or compressed.

 

The amount of elastic potential energy is determined by how hard it is to compress or stretch something and how far it is stretched or compressed.

 

The equation to find this is:

PE = 1/2kd²

where PE is potential elastic energy, k is a constant specific to a particular stretchy thing (spring, rubber band, etc.) and d is the distance that it is stretched or compressed (sometimes x is used instead of d, as in the illustration)


Regarding Potential Energy and Kinetic Energy, remember that they both deal with either the potential to create motion or deal with the actual motion.

Thermal Energy—the total potential and kinetic energy associated with the motion of all the molecules in an object.

Understanding thermal energy relies on what was learned about the kinetic theory of matter: all objects are made up of particle that are in constant motion. When temperature increases, the molecules move faster (and take up more room).
Thermal energy is the sum of all the kinetic energy of all those molecules.

The molecules of different types of material act differently in reaction to thermal energy, but working with thermal energy is fun and relatively easy. This will be addressed later in detail.

Chemical Energy—the energy stored in the chemical bonds of a substance.

If the bonds can be broken, the energy is released. Burning is the process of creating a chain reaction of bonds breaking and giving of energy—the chemical energy is converted into light and heat.

Electric Energy—the energy associated with electric charges.

Electric energy can be converted (through use of a motor) into mechanical energy. Mechanical energy can be converted (through a generator) into electric energy. Electric energy can be converted into light and heat by a light bulb.

Electromagnetic Energy—a form of energy that travels through space as a wave.

Light is electromagnetic energy.

Nuclear Energy—the energy stored in atomic nuclei.

It takes energy to slam protons and neutrons together in a nucleus. Once the nucleus is formed, that energy is stored in the nuclear bonds. Breaking those bonds (fission) releases the energy.


SUMMARY

There is a close relationship between force, work, and energy. Energy is the potential to do work, and can be seen in different forms.
_______________

Definitions and content from:

New Oxford American Dictionary

Physical Science Concepts in Action, Pearson 

http://hyperphysics.phy-astr.gsu.edu/hbase/pespr.html