Biology Index
Where are we going with this? The information on this page should increase understanding related to this standard: Explore the process of mitosis understanding why mitosis happens, the main goal of mitosis, and the key terms involved in mitosis.
Article includes ideas, images, and content from Troy Smigielski (2021-11)
Meiosis
(So, this is not the same as mitosis?)
Review of Mitosis Basics
"Mitosis is a process where a single cell divides into two identical daughter cells (cell division). During mitosis one cell? divides once to form two identical cells. The major purpose of mitosis is for growth and to replace worn out cells" (
Souce, 2021-11)
So, cells split… hmm…
Introducing Meiosis
Meiosis is very similar to mitosis. In some ways. However, it is not the same.
"Meiosis is a type of cell division that reduces the number of chromosomes in the parent cell by half and produces four gamete cells. This process is required to produce egg and sperm cells for sexual reproduction. ... Meiosis I is a type of cell division unique to germ cells, while meiosis II is similar to mitosis"
(Source, 2021-12).
The simplest difference between the two is that mitosis divides one time while meiosis divides two times (Meiosis I and Meiosis II).
The main goal of meiosis is to create gametes, which are sex cells (1n). In males, meiosis produces sperm. In females, meiosis produces eggs.
Each gamete has half the number of chromosomes as the original cell. Why?
In sexual reproduction, the sperm and egg combine to create one cell, and that created cell needs to have the right number of chromosomes. So… Human cells have 46 chromosomes. The egg and sperm, then, need to have 23 each, half the number of the original cells, so that they can combine into the correct number (because math).
So, to reiterate, the main goal of meiosis is to create cells used in reproduction—the sex cells.
A Closer Look At Meiosis
The phases of meiosis are nearly identical to mitosis with a few exceptions.
The first major difference is that there are two divisions.
In meiosis, there is no Interphase II!
There is no Interphase II because DNA replication happens in Interphase, and the purpose of meiosis is to create haploid cells with half the DNA as the original cell.
It is in interphase that the chromosomes double. If there was a second interphase, then the the number of chromosomes would not change. Well, that would defeat the purpose, now wouldn't it?
Note: after Meiosis I, both cells still have 46 chromosomes. Also, the cell does not grow before Meiosis II because there is no G1.
If Interphase II occurred, you would never be able to create a gamete (a haploid cell that only has 23 chromosomes).
The Process of Meiosis
At the beginning, you have a pair of matching chromosomes (1 from mom; 1 from dad) called homologous chromosomes. Homologous chromosomes are also called homologs.
 |
(Source, 2021-12)
The word comes from the Greek words, "homo" and "logos" meaning
to have the same composition, arrangement, order, ratio, or proportion.
|
So… let's talk about the homologs a little, and use humans as the example. Each human cell has 46 chromosomes. Okay? But!!! It is actually 23 pairs of homologs. One chromosome in each homologous pair comes from the mother and one chromosome in each pair comes from the father.
Think of the homolog as a chromosome pair that has genetic information about certain aspects of the organization. For instance hair and eye color are parts of a certain chromosome. Each human cell has one of these chromosomes from the mother and one of these from the father.
So there are 23 different types of chromosomes and you get one of each type from the mother and one of each type from the father. A homolog is any two chromosomes of the same type.
How about we get a little ridiculous? Say of the 23 types of chromosomes, we have
Milkshake chromosomes
Hamburger chromosomes
French fry chromosomes
Apple pie chromosomes
and 19 others
If you take the dad-milkshake and the mom-milkshake, that's a homolog.
If you take the dad-hanburger and the mome-hamburger, that's a different homolog.
… and so on…
You have 2 complete sets of 23 different chromosomes: a dad set and a mom set.
Let's run with this analogy a little… At the beginning of meiosis, you have one dad-milkshake chromosome and on one mom-milkshake chromosome. One homolog.
So, back to meiosis…
Each homolog duplicates in Interphase I.
Homolog duplication creates a special connection of two pairs of homologs called a tetrad. The tetrad is a duplicated copy of mom’s chromosomes attached to a duplicated copy of dad’s chromosomes.
After Interphase I, you have two dad-milkshake chromosomes and on two mom-milkshake chromosome. Two homologs. Plopped atop each other. That's a tetrad. You have one cell with 4 milkshake chromosomes: 2 dad-milkshakes, and 2 mom-milkshakes.
What is that prefix, "tetra"?
Tetra means four. Therefore, a tetrad is an arrangement that includes four pieces. (Wait! I thought quad means four! Oh, just… nevermind.)
The tetrad is a very important structure (as will be discussed as we go). It is recognizable by the two pairs of homologs that are attached to each other. This will frequently be represented in images such that it looks like two X's clost to each other or even overlapping.
At this point, the only difference between mitosis and meiosis is that the homologs are attached to each other. The homologs are not attached to each other in mitosis. This is why they are called sister chromatids and not a tetrad.
This brings the process to the end of interphase and into the actual dividing process. Remember, there will be two divisions: Meiosis I and Meiosis II.
During Meiosis I (the first division), homologs (homologous chromosomes) are separated. This creates 2 cells with 2 chromatids in each.
Notice how each cell is identical to the parent cell. This is pretty much mitosis, except the homologs are attached (tetrad).
After Meiosis I, you still have two dad-milkshake chromosomes and two mom-milkshake chromosome. However, the Tetrad has been pulled apart into different cells.
Now, you have two cells, but still with 4 milkshake chromosomes: 1 dad-milkshake and 1 mom-milkshake chromosome in EACH of the two cells.
NOTE: Something else happens in Prophase I that sort of mixes things up. You can think of it as the milkshakes swapping straws and lids with each other. Sorta. More later on this!
The image above simplifies the process. Meiosis actually follows the four phases of cell division seen in mitosis: prophase, metaphase, anaphase, and telophase.
Remember that there is no Interphase II. After Meiosis I, the cell will not undergo Interphase II because the cell does not want DNA replication.
This goes back to the purpose of creating two "half cells" that can be joined to become a "whole cell." More accurately, Meiosis creates two bodies (gamites) that have half of the chromosomes which, combined, create a cell with all of the chromosome pairs.
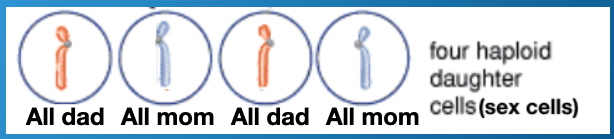
In Meiosis II (the second division), sister chromatids are separated. This creates 4 cells with 1 chromatid each.
These resulting cells are gametes.
After Meiosis II, you still have two dad-milkshake chromosomes and two mom-milkshake chromosome. However, they are now in 4 different cells
Now, you have four cells, but still with 4 milkshake chromosomes: 1 dad-milkshake in two of the cells and mom-milkshake chromosome in two of the cells.
NOTE: However, in Prophase I they mixed up a little… swapped lids and straws, sorta More later on this!
In Meiosis II, the cell undergoes all 4 main phases, as it did in Meiosis I.
In women, 3 gametes are inactivated, and these are called polar bodies. The remaining one is used for reproduction or shedding.
So, that's pretty much what happens! Not too bad!
However, there is a little twist. Actually, not so much twisting but rather crossing over!
This is the little mixing up mentioned in earlier milkshake examples.
Previewing Genetics
After the process of meiosis is complete, there are four "things" that are produced, granddaughters of the original cell. The "things" are called gametes. They are sort of half-copies of the original cell. Sort of not. That's where crossing over comes in.
But, before we talk about the crossing-over process… let's sidestep a little…
Remember: Your cells have 23 chromosomes from your mom and 23 chromosomes from your dad. If you were to have a child, which one gamete of the four produced would you pass on?
Neither, you would pass on one that had a mixture of your mom and your dad’s chromosomes. How do we get a “mixture”?
The tetrad formation back in Prophase I provides an opportunity for chromosomes to trade parts in a process called crossing over.
 |
After crossing over, one of the gametes from the father has some of the genetic material from the mother and one of the gametes from the mother has some of the genetic material from the father.
Stop and look at the image again. Longer… |
Crossing over occurs in Prophase I, and greatly increases genetic variability.
How?
Looking Closer at the Cross-over Process
Traits in an organism come from the genes in the DNA, which is organized into chromosomes. Each chromosome carries multiple genes in specific segments of DNA.
To say that differently, "A gene is a region of DNA that encodes function. A chromosome consists of a long strand of DNA containing many genes. A human chromosome can have up to 500 million base pairs of DNA with thousands of genes" (
Source, 2021, 12)
So from the mother and father we have in humans 23 pairs of matching chromosomes. Each pair of chromosomes have the same sequences of genes.
Let's use hair color as an example. The gene for human hair color is called MC1R. This gene is located on chromosome 16.
So, in Prophase I, two chromosome 16s from the father and two chromosome 16s from the mother form a tetrad. There are four full chromosomes in the tetrad.
Almost certainly, the father's gene MC1R and the mother's gene MC1R are different. The different variants of a gene are called alleles.
During crossover, some of the alleles from the father chromosomes swap places with the corresponding alleles from the mother chromosome. The resulting chromosome, thus, has the same DNA sequence, but the code for some traits are switched from the father's chromosome to the mother chromosome.
So, after Prophase I, there are still four chromosomes, but they are no longer identical to either the mother's or father's. Ultimatly, by the end of Meiosis II, the four haploid cells produced contain a mixture of the parents' genes.
The end result of meiosis is that:
1. Beginning with one diploid cell having pairs of homologs (one mother chromosome and one father chromosome,
2. you end up with four haploid cells having one copy of a chromosome from each pair,
3. but the copies are partially mixed up.
____________________________
Summary and Review
Meiosis divides a diploid (2n) cell into four haploid (1n) cells called gametes.
Each daughter cell has half the number of chromosomes as the original.
Recall that in mitosis, each resulting cell has the same number of chromosomes as the original. In meiosis, each resulting cell has half the number of chromosomes as the original.
Mitosis vs. Meiosis Review
- In meiosis, matching chromosomes duplicate and stay together, forming a tetrad.
- The phases of meiosis are very similar to those in mitosis, with a few exceptions.
- Crossing over happens in Prophase I
- There is no Interphase II because Meiosis II does NOT replicate DNA.
How does mitosis and meiosis work together?
Some example images…