So… In baseball and softball, many batters batters hate the curveball… Because it curves…
NOTE: The physics of this is true for ALL sports where a ball moves through the air… tennis, golf, ping pong, volleyball, soccer (bend it like Becker)…
Now, the curve in question is in addition to the fact that it is moving from the picture to the batter as a projectile which automatically means that it's up and down is changing at the same time it moves closer and closer to the batter.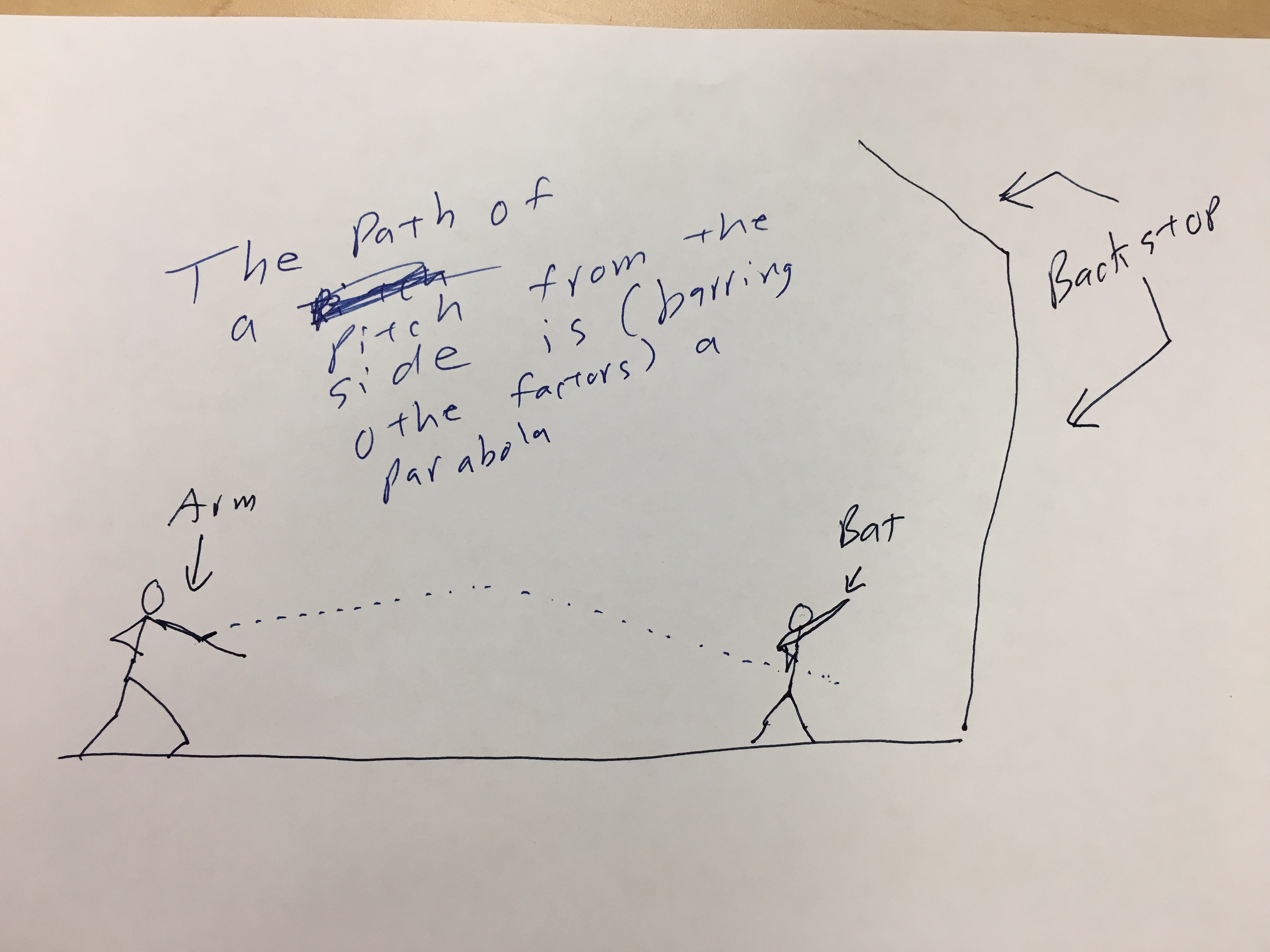
Imagine slow-pitch softball or a lobbed pitch… In the extreme, think about soft toss… The ball moves up and down as it approaches the strike zone.
So, every pitch regardless of type is, from the moment it is released affected by these three forces:
- Gravity pulls the ball down toward the center of the earth.
- There is a tiny, tiny buoyant force that is far far less than the force of gravity.
- There is air resistance (friction) that opposes the motion of they ball and which is always directly directly opposite the direction of the instantaneous velocity.
Now, let's talk about rotation! Because, except for a knuckle ball, pitches rotate…
I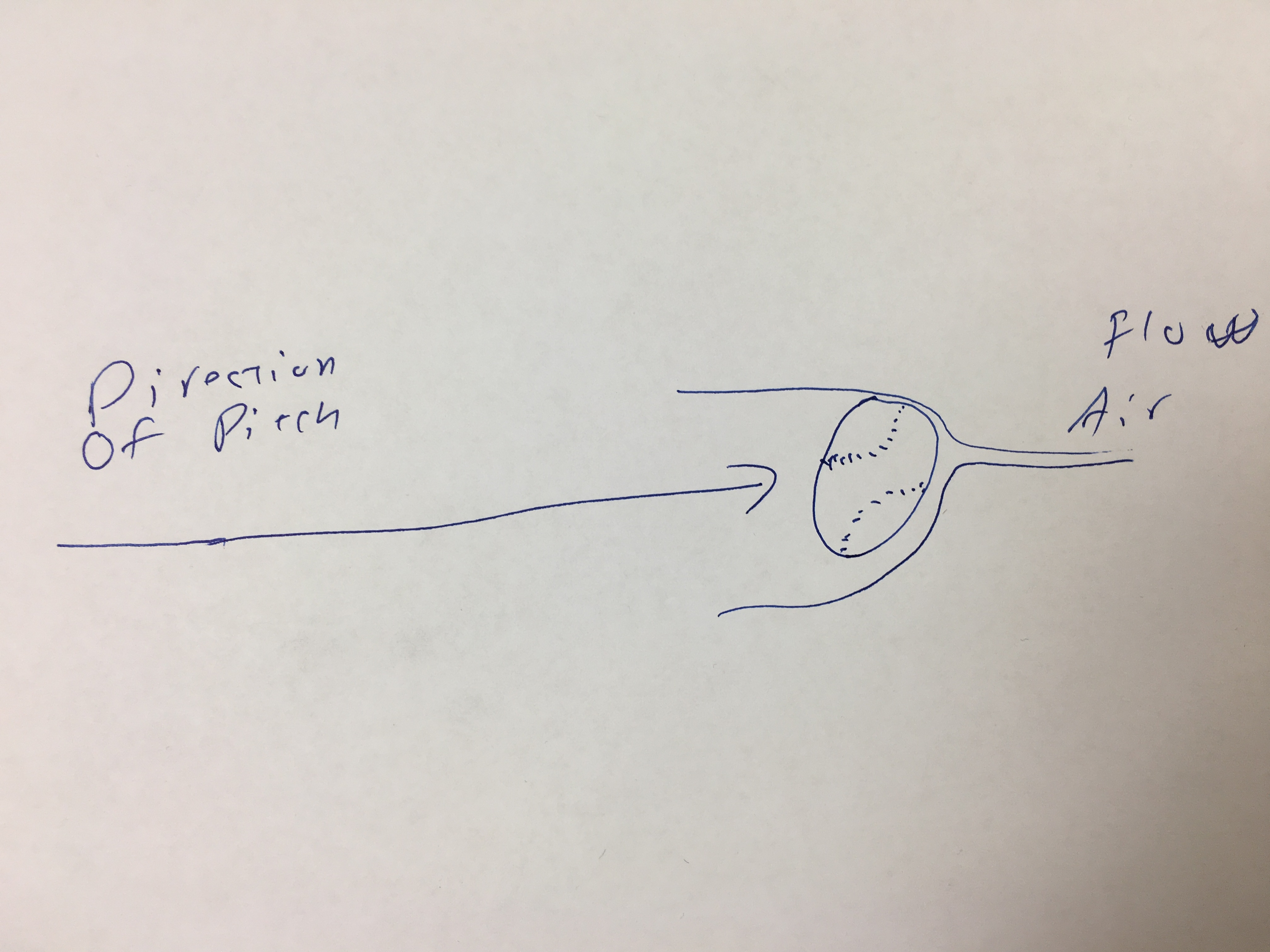 magine a ball spinning on an axil, not moving. When the ball spins, the air around it is "drug" in the direction of the spin. Now, if you add in the movement of the ball, something happens!
magine a ball spinning on an axil, not moving. When the ball spins, the air around it is "drug" in the direction of the spin. Now, if you add in the movement of the ball, something happens!
First if the ball is thrown and spin is ignored, you get an object moving through the air. The air flows around the ball equally. Nothing interesting there…
However, if you account for the spinning of the ball… and the air that is being drug around it by the spin, you start to see something.
When air moves faster, is gets stretched out. There are fewer molecules of air in the same space. From the gas laws, it is known that if you have fewer molecules in the same space, the pressure is lower (given constant temperature, which can be assumed over the diameter of a baseball or softball).
The result is that one side of the ball has high pressure and the other side has low pressure. The difference in pressure creates a force. The air pressure difference pushes the ball form the high pressure region to the low pressure region.
That is to say there is a force acting in the direction of the low pressure. Given Newton's Second Law, it is known that F=ma, so where there is a net force, the ball must accelerate (change velocity) in the direction of the force.
Thus, the rate of acceleration can be found based on some function of the difference in pressure (F) divided by the mass of the ball:
a = ƒ(p1 and p2)/m
So, what can a pitcher do to make the ball curve? Well… you can't control the mass of the ball. You can control, however the spin.
Since the air moving around the ball due to it moving is the same on all sides, the spin accounts for the difference in pressure. Both p1 and p2 are affected by the spin
T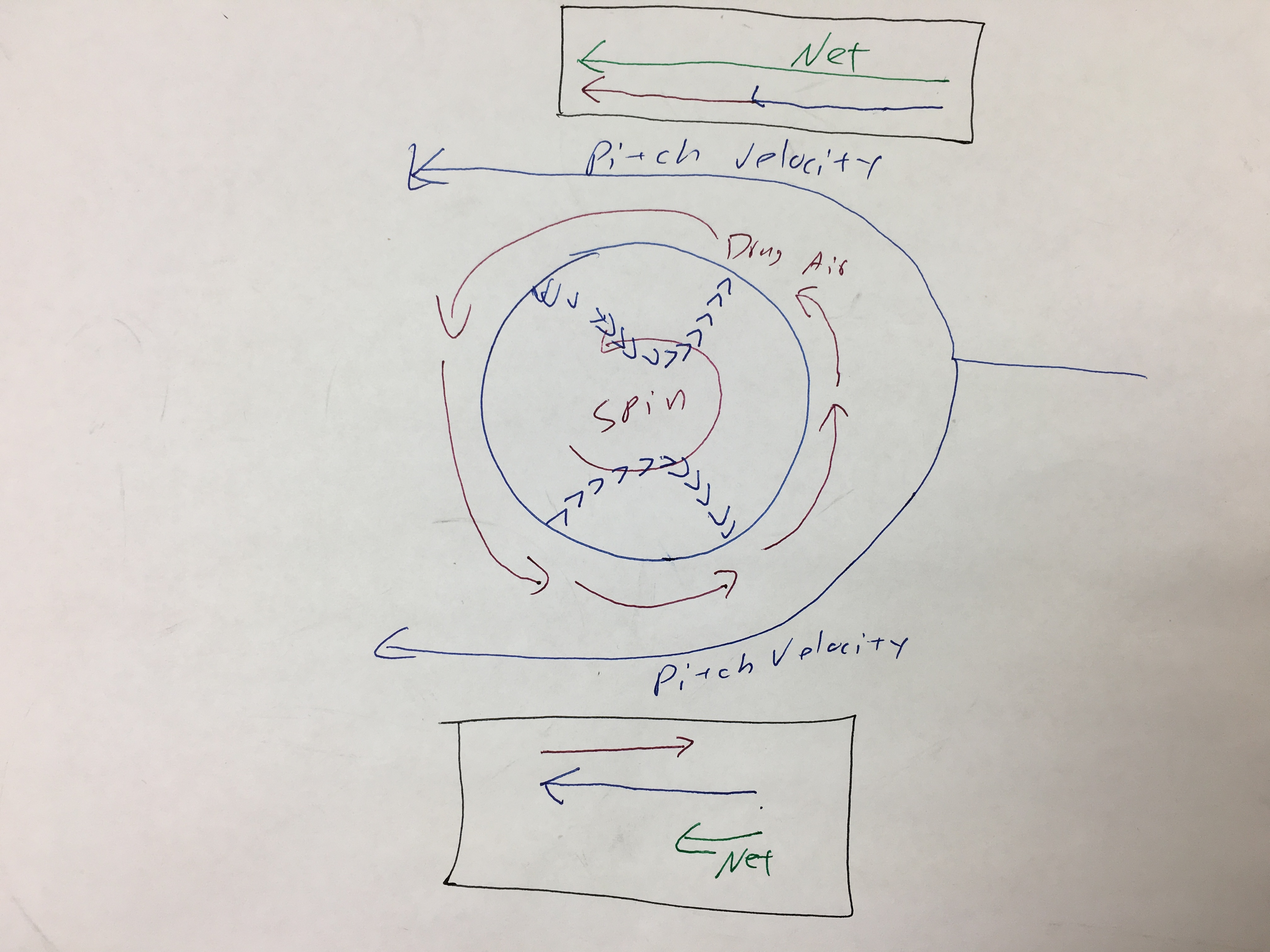 he net air flow is on one side pitch velocity + drug air.
he net air flow is on one side pitch velocity + drug air.
The net air flow on the other side is pitch velocity - drug air.
Thus, since the difference in pressure is a result of the DIFFERENCE in the net velocities of the air on opposite sides of the pitch path, the more spin, the bigger the difference in pressure.
AND, then, the bigger the difference in pressure (back to the math)…
a = ƒ(p1 and p2)/m
…the greater the rate of acceleration.
By controlling the spin allows a pitcher to control where the high and low pressure zones are. The ball will break into the low pressure zone.
A pitch, then, with backspin, will dive. If the rotation is the other way (e.g. a good overhand throw), the ball will actually float some and the effect of gravity will be lessoned.
The LESS the axis of rotation aligns with the path of the ball, the GREATER the affect of the spin on the ball's path.
Conversely, if the axis of rotation aligns with the path of the ball's movement, then the affect of the spin is zero. Think of a spiral football pass. IF the pass/punt spirals properly, the affect of the spin is zero.
An overhand fastball rotates back toward the pitcher. Thus, there is low pressure on top of the ball.
An underhand fastball (or a topspin tennis shot) rotates forward toward the batter. Thus, there is low pressure on the bottom of the ball.
Cutters, sliders, etc have various spins that move the low pressure zone to different places on the ball.
CONCLUSION:
1.) Since the rate at which a ball's velocity changes can be found by
a = ƒ(p1 and p2)/m
and since the difference in pressures is caused by the spin, then changing the direction and rate of the spin will change the direction and rate of the acceleration (of the break).
2.) Increasing the rate of spin increases the difference in pressures. The greater the difference in pressure, the more the ball with break (accelerate).
Additional Notes:
1.) The diameter of the ball affects the velocity of the spinning surface. Thus, two balls of the same mass spinning at the same rate, but having different diameters will break differently. For example, a huge beachball with the same mass as a volleyball will curve more with the same spin.
Additional Notes:
1.) The diameter of the ball affects the velocity of the spinning surface. Thus, two balls of the same mass spinning at the same rate, but having different diameters will break differently. For example, a huge beachball with the same mass as a volleyball will curve more with the same spin.

