Where are we going with this? The information on this page relates to the skills needed to investigate and evaluate the graphical and mathematical relationship (using either manual graphing or computers) of one-dimensional kinematic parameters (distance, displacement, speed, velocity, acceleration) with respect to an object's position, direction of motion, and time.
Projectile Motion
When Vertical Displacement Is Not Zero
Why is this even a thing!
 |
| Source 2021-10-25 |
What happens if a projectile is set into motion, but from a position above the horizontal? Like in shot putting.
The shot is launched from a distance of around 2.25 meters above the ground. How does this change the calculations?
The problem starts out just as if the projectile began on the ground.
The difference occurs in step 4 (below). Because the vertical displacement is NOT ZERO, the projectile has further to go before hitting the ground.
tdown is now NOT EQUAL to tup.
Keep in mind that you COULD use this method, even if the initial distance is zero. You would just get the same number for time up and time down.
With that in mind, let's get going…
______________________________
STEP 1: Draw and Label
STEP 2: Find the y and x components of the velocity v where the angle is θ.
v • cosθ = vx
v • sinθ = vyi
Whereas the velocity up/down will change due to gravity, it will carry the subscript i for "initial."
Whereas we are ignoring air resistance, vx is a constant.
STEP 3: Find time up:
To find time up, use the velocity equation…
vf = vi + at
Plug in for the specific situation…
0 = vyi + (-9.81)tup-vyi = -9.81•tup-vyi /-9.81 = tup
vyi /9.81 = tup
Find time down:
To find tdown, you will need to use the distance equation:
df = di + vit + 1/2at2
The most accurate way to think about this is to say df is the ground and di is the total vertical displacement, dy(max) which is how much the projectile went up (∆dy) plus the initial vertical displacement (dyi). Since these would be measured from the ground to the top of the trajectory, they would be positive meaning a is in the opposite direction and is negative. Further df would be when it hits the ground and would be zero.
Did you notice that, to find time down, we have to find max vertical displacement (which we'll call dy(max))?
To do that, we will ALSO use the distance equation, but with the value for tup which we found in Step 3.
STEP 4: Find how high it goes.
We use that value, tup, in the distance equation to find how high it goes, dy(max).
df = di + vit + 1/2at2
Plug in for specific case:
dy(max) = dyi + vyi•tup + 1/2at2
STEP 5 Find time down
Now that we know how high it went, we can use the distance equation AGAIN to find tdown with the following values.
df = 0 m (the ground)
di = dy(max)
vi = 0 m/s (because we are measuring from when it stopped going up, max distance in y direction)
a = g = -9.81 m/s/s (or -9.8 m/s/s)
t = tdown
Solving for t we find that…
df = di + vit + 1/2at20 = dy(max) + 0 • tdown + 1/2(-9.81) tdown2-dy(max) = -4.905 tdown2-dy(max) / -4.905 = tdown2
The negatives cancel. Take square root of both sides:
tdown = √ (dy(max)) / 4.905
STEP 6: Find the total time:
ttot = tup + tdown
STEP 7: Find the horizontal displacement, dx:
Whereas…
di = dxi = 0
vi = vx (From Step 2)
a = 0
t = ttot
df = di + vit + 1/2at2
dx = 0 + vx•ttot + 0
dx = vx•ttot
______________________________
By now, you will have noticed that there are a lot of steps and a lot to understand.
Conceptually, it's not too hard:
The horizontal distance is how far it goes before it hits the ground, and is found easily:
dx = vx•ttot
"Before it hits the ground" (ttot) is how long it takes to go up added to how long it takes to come back down.
It is in the most complicated steps (3 and 4) that we find the "how long it takes".
Conceptually, it might help to partition off parts of your paper to do a few things…
1. Draw it out and find vx and vyi…2. Make a box in which you will find dx (at the end of the process)3. Figure out the time up and time down then go back to the box…
Once you get through the process conceptually a few times, you can fall into a "calculator" process (though you'll still need to write down some values as you go." Consider the checklist that follows…
CHECKLIST/SUMMARY
So, if you are given theta and the velocity, here's a checklist sort of process…
- #1 Draw the diagram and label everything.
- #2 Find the component velocities in the x and y directions:
v • cosθ = vxv • sinθ = vyi
- #3 Find the time up using vy and acceleration due to gravity (probably 9.81 m/s/s)
tup = vyi / 9.81
Find the time down:
• #4 Find how high it goes
- First, find dy(max):
dy(max) = dyi + vyi • tup + 1/2•(-9.81)•tup2 - #5 Find time down
- Then, find tdown:
tdown = √ dy(max) / 4.905
- #6 Find the total time where…
ttot = tup + tdown
- #7 Use the distance equation to find the horizontal displacement:
dx = vx•ttotwhere vx was found in step 2 and t was found in step 4.
Something like this…
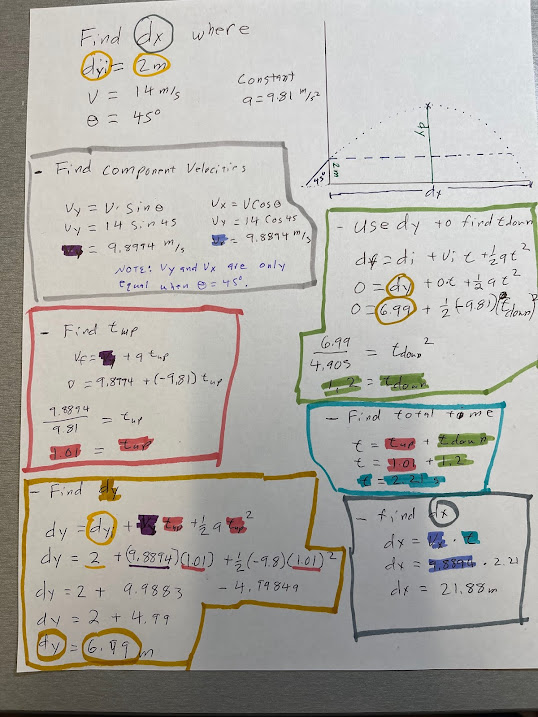 |
| The scribbling above follows the steps without labeling them with numbers. Go down the left, the back up and down the right. |
How about with colors?
CHECKLIST/SUMMARY
So, if you are given theta and the velocity, here's a checklist sort of process…
- #1 Draw the diagram and label everything.
- #2 Find the component velocities in the x and y directions:
v • cosθ = vxv • sinθ = vyi
- #3 Find the time up using vy and acceleration due to gravity (probably 9.81 m/s/s)
tup = vyi / 9.81
Find the time down:
• #4 Find how high it goes
- First, find dy(max):
dy(max) = dyi + vyi • tup + 1/2•(-9.81)•tup2 - #5 Find time down
- Then, find tdown:
tdown = √ dy(max) / 4.905
- #6 Find the total time where…
ttot = tup + tdown
- #7 Use the distance equation to find the horizontal displacement:
dx = vx•ttotwhere vx was found in step 2 and ttot was found in step 4.


No comments:
Post a Comment