The concepts of
force,
work, and
energy are closely related, and they are often tied to
motion. To begin understanding of how they interact, it is important to start with a firm grasp of the basic concepts.
FORCE
The starting place for understanding how force, work, and energy interact is to quickly review
concepts related to force.
Force is a push or a pull that acts on something in creation.
Forces are the result of four fundamental forces found in creation: gravitational force, electromagnetic force, and the strong and weak forces associated at the atomic level.
At any given time, an object in the universe is subjected to many forces. Forces on an object add up as vectors (direction and magnitude), and if the net force is NOT zero, then the object will be accelerated at a rate given by Newton's second law:
F = ma
where
F is the net force on an object,
m is the mass of the object, and
a is the resulting acceleration.
Force is measured in Newtons (the symbol is N), which is the potential to accelerate a 1 kg object at a rate of 1 meter per second per second. that is:
1 N = 1 (kg • m/s)/s = 1 kg • m/s2
It is important to remember that an object can be moving, but that the net force on it is zero. This does not mean there are no forces at work. It just means that it is moving at a steady rate (constant velocity) because all of the forces are balanced out. For example:
Pedaling a bicycle at a steady rate requires that the force of the tires pushing against the ground is equal to the wind resistance opposing the motion of the bike.
When a box is pushed across the floor at a steady rate, the force pushing against the box is equal to the oppositional force of friction.
Consider the box example further. The force of gravity pulls the box toward the center of the earth, causing it to press against the floor. The solid nature of the floor opposes the force of gravity, keeping the box from moving downward. The "up and down" forces are in balance, and they create the resistance of friction that opposes the force exerted on the box to push it. If the pushing force is greater than the frictional force, then the box accelerates. If they pushing force is equal, the box moves at a steady rate. If the pushing force is less than the force of friction, the box slows down or does not start moving.
WORK
Extending the concept of force to motion, the idea of work emerges.
In the context of physics,
work is a very specific concept.
Work is the quantity that represents the application of a force through a distance. This means that
work is done when a
force is exerted and when
motion occurs. Pushing against a wall does no work, though it requires a lot of effort (which is a loosely used term related to work, force, and motion.
Work can be calculated as the product of force and distance/displacement:
W = Fd
where
W is work,
F is force applied (not net force!), and
d is displacement/distance.
Work is measured in Newton-meters (the symbol is Nm or N-m) meaning that a Newton was applied through a distance of one meter.
So, back to the box example above, if the force to push the box causes it to move some distance, then work is done. If the force does not cause it to move, then effort was spent, but no work was done.
Assume the force needed to balance friction and move the box at a constant velocity is 5 N and that the box is pushed 10 m. In that case how much work was done?
W = Fd
W = 5N • 10 m
W = 50 Nm
It is vital to remember that
work is done, not as a result of the net force, but rather as a result of the applied force through a distance. In the case of a box moving at a steady rate (constant velocity) the net force on the box is zero, but the applied force is used to find
work done.
To make things slightly confusing, in many cases, (because of what is discussed below about energy), work will given the unit of joules (J). To extend the above example with this concept,
W = Fd
W = 5N • 10 m
W = 50 Nm
W = 50 J
ENERGY
Going to the next concept, energy, is not terribly difficult.
Energy can be defined as the potential to do work.
There is, thus, a direct relationship between
work and
energy. However, where work is often described with the unit of Newton-meters, energy is generally described with the equivalent unit, joules (the symbol is J).
A joule is the energy needed to do 1 Newton-meter of work. So:
1 J = 1 Nm
An example will help clarify the relationship between work and energy. Think about this:
If "Cash" is the potential do "pay" and
energy is the
potential do work, then…
Q: If you paid $20.00 for something, how much cash did you spend?
A: You spent $20.00
Q: If you did 20 Nm of work, how much energy did you spend?
A: You spent 20 Nm (or 20 J)
Thus, once you have calculated the amount of work done, you know how much energy was used to do it.
FORMS OF ENERGY
Up to this point, energy has been looked at in terms of motion and the potential to cause motion. However, energy exists on other forms. It is important to understand that energy can change forms.
Energy exists in different forms. Though it is still the potential to do work, as different forms of energy are examined, the idea of moving something through a distance can get lost. That should not be a distraction, though. Just cling to the idea that energy is the potential to do work.
Mechanical Energy—This is the form of energy that has been discussed up to this point.
Mechanical energy is the energy associated with the motion and position of everyday objects.
There are three TYPES of Mechanical Energy
In the sections that follow, three types of mechanical energy will be explored:
- Kinetic energy
- Gravitational potential energy
- Elastic potential energy
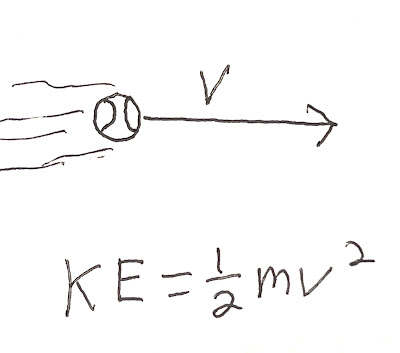
Kinetic Energy—the energy of motion is called kinetic energy.
The amount of energy a moving object has can be found based on the mass and velocity of the object that is moving. Kinetic energy (KE) is found with this equation:
KE = 1/2 mv2
where KE is kinetic energy, m is mass and v is velocity.
Potential Energy—energy that is stored as a result of position or shape.
Potential energy (PE) is a little more broad than kinetic energy. Potential energy can be thought of as how much motion could occur if the stored energy was released.
For instance, a hot wheel car at the top of the track is not moving, but if it is released, because of its position, gravity will cause it to start. The car will accelerate (overcoming friction of the track and in the bearings of the wheels) and move down the track.
Another type of potential energy relates to the shape of something. When you stretch a rubber band, because of its shape, it has stored, potential energy. Likewise a compressed or stretched spring, because of its shape, also has potential energy.
Two types of potential energy will be examined more specifically.
Gravitational Potential Energy—the potential to create motion based on position within gravity and on the mass of the object.
Imagine hanging a heavy weight over a pulley and attaching to a car. Letting the weight go would create tension in the rope and that tension would create a force on the car causing it to accelerate. The higher the weight, the more potential it would have. The heavier the weight, likewise, the more potential it would have.
The potential gravitational energy can be found with this equation:
PE = mgh
where PE is potential gravitational energy, m is mass, g is acceleration due to gravity, and h is height.
On earth, acceleration due to gravity is 9.81 (m/s)/s.
Elastic Potential Energy—the potential energy of an object that is stretched or compressed.
The amount of elastic potential energy is determined by how hard it is to compress or stretch something and how far it is stretched or compressed.
The equation to find this is:
PE = 1/2kd2
where PE is potential elastic energy, k is a constant specific to a particular stretchy thing (spring, rubber band, etc.) and d is the distance that it is stretched or compressed (sometimes x is used instead of d, as in the illustration)
Regarding Potential Energy and Kinetic Energy, remember that they both deal with either the potential to create motion or deal with the actual motion.
Thermal Energy—the total potential and kinetic energy associated with the motion of all the molecules in an object.
Understanding thermal energy relies on what was learned about the kinetic theory of matter: all objects are made up of particle that are in constant motion. When temperature increases, the molecules move faster (and take up more room).
Thermal energy is the sum of all the kinetic energy of all those molecules.
The molecules of different types of material act differently in reaction to thermal energy, but working with thermal energy is fun and relatively easy. This will be addressed later in detail.
Chemical Energy—the energy stored in the chemical bonds of a substance.
If the bonds can be broken, the energy is released. Burning is the process of creating a chain reaction of bonds breaking and giving of energy—the chemical energy is converted into light and heat.
Electric Energy—the energy associated with electric charges.
Electric energy can be converted (through use of a motor) into mechanical energy. Mechanical energy can be converted (through a generator) into electric energy. Electric energy can be converted into light and heat by a light bulb.
Electromagnetic Energy—a form of energy that travels through space as a wave.
Light is electromagnetic energy.
Nuclear Energy—the energy stored in atomic nuclei.
It takes energy to slam protons and neutrons together in a nucleus. Once the nucleus is formed, that energy is stored in the nuclear bonds. Breaking those bonds (fission) releases the energy.
SUMMARY
There is a close relationship between force, work, and energy. Energy is the potential to do work, and can be seen in different forms.
_______________
Definitions and content from:
New Oxford American Dictionary
Physical Science Concepts in Action, Pearson
http://hyperphysics.phy-astr.gsu.edu/hbase/pespr.html